Magic square 3x3 with negative and positive integers

SOLVE The 3x3 Magic Square Completely - There Can Only Be One. Let us discuss that The figure shown below represents a magic square where abc are integers.

Given s convert it into a magic square at minimal cost by changing zero or more of its digits.

Magic square 3x3 with negative and positive integers. How do you remove black magic placed on you well let me start off saying that black magic or black art spells is a form of negative energy as far as how to remove black magic spells that has been cast on you well first you will need to think positive things about your self and believe in your self and believe that good will over come evil Now second you will need to do a little meditation and focus on positive. How do I create a 3x3 magic square with negative and positive numbers. Draw a 3 x 3 Grid.

Extend the grid as shown and write integers from 1 to 9 in pattern as shown. Excluding reflections and rotations there is only one 3x3 magic square using 1-9. What two numbers when using one negative number when multiplied together equal 405.

Since 405 is positive. Show activity on this post. Turns out you dont have enough information – but you could put anything you wanted in any other cell.

As shown by Joe Z in this answer all 33 magic squares can be expressed as. B 2 b 2 c 3 a c 2 c a b c a 2 b a 2 b c. Magic Squares with Positive and Negative Numbers.

In this worksheet students solve problems with positive and negative numbers using Magic Squares. Use Four Operations for All Numbers. We define a magic square to be an n x n matrix of distinct positive integers from 1 to n 2 where the sum of any row column or diagonal of length n is always equal to the same number.

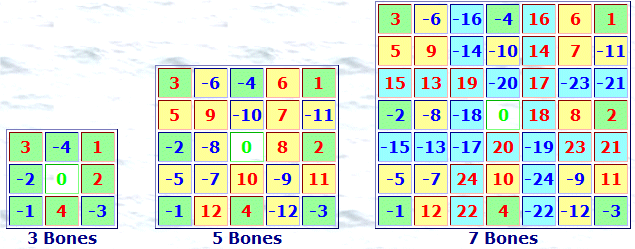
You will be given a 3 x 3 matrix s of integers in the inclusive range 1 9We can convert any digit a to any other digit b in the range 1 9 at cost of a b. A magic square consists of distinct integers such that the sum of integers in any horizontal vertical or main diagonal is always the same magic constant. Two such magic squares consisting of distinct positive and negative integers are shown below-Now the question arises how to form a magic squares.

Let us discuss that The figure shown below represents a magic square where abc are integers. How Many 33 Magic Squares Are There. There are 8 ways to make a 33 magic square.

In fact there is really only one pattern. Every other pattern is a rotation or reflection. From the upper left the first square on the right is a reflection.

Create a 3x3 Magic Square that uses integers from -10 to -2. By the way this is a weird magic square since diagonals dont need to match the common sum. I dont know how to create a magic square and would very much appreaciate anyones help.

I found this-4 -4 -2-4 -2 -4-2 -4. Solve the square then replace the integers with the original integers in the problem you were given. So if its a 3x3 square with integers from -4 to 4 turn it into a regular 3x3 square solve it and replace 1 in the final solution with -4 replace 2 with -3 replace 3 with -2 etc.

In magic squares all of the rows columns and diagonals add up to the same number. Magic squares like this one where we have negative numbers as well work. Welcome to our TES shop.

We aim to make resources that help students to gain maximum feedback as they work challenge their misconceptions and develop their understanding. Please also check out our website wwwMathsPadcouk. A set of magic squares for students to practise adding negative integers.

The work of Eulerimplies already thatthere can be no 3x3 magic square with entries which are cubes. If z3is the number in the centre cell then any line going through the centre shouldhave x3 y3 2z3. Euler and Legendre39demonstratedthat x3 y3 kz3is impossible with distinctintegers for k 1 2 3 4 5.

A Magic Square is a n x n matrix of distinct element from 1 to n2 where the sum of any row column or diagonal is always equal to same number. Consider a 3 X 3 matrix s of integers in the inclusive range 1 9 We can convert any digit a to any other digit b in the range 1 9 at cost a b. Given s convert it into a magic square at minimal cost by changing zero or more of its digits.

A magic square of order n is an arrangement of n 2 numbers usually distinct integers in a square such that the n numbers in all rows all columns and both diagonals sum to the same constant. A magic square contains the integers from 1 to n 2. The constant sum in every row column and diagonal are called the magic constant or magic sum M.

The magic constant of a normal magic square. Heres a magic square with a twist. Use this memory technique to help your students remember the rules for multiplying and dividing positive and negative integers.

Rules and examples organized into an easy-to-read chart An exploration activity for creating the magic sq. SOLVE The 3x3 Magic Square Completely - There Can Only Be One. Use this worksheet to complete magic squares using negative numbers.

Magic squares are one of the simplest forms of logic puzzles and a great introduction to problem solving techniques beyond traditional arithmetic algorithms. These are 4 magic squares that can be used to practise adding positive and negative numbers. There are 3 major properties of Magic Square and on the basis of these properties Magic Square Puzzles can be solved.

The Addition Law of Magic Square describes that when you add same number to the numbers present in Primary or Standard or Derived Magic Square puzzle the result will be a Magic Square with a new Magic Constant. This can be illustrated with the figure below. Prime Number Pan-Magic Square Maker Make Your Own.

This page allows you to choose any size from 5x5 to 97x97 provided it is a prime number. You can also vary the length of the Knights MoveThe other pages in this section allow you to experiment and enter your own values - select 3x3. 3x3 magic squareA magic square is an arrangement of the numbers from 1 to n2 n-squared in an nxn matrix with each number occurring exactly once and suc.